算法分析系列文章中的代码可被任何人无偿使用于任何场景且无需注明来源也不必在使用前征得本文作者同意。

算法分析系列文章旨在传播准确、完整、简洁、易懂、规范的代码实现，并传授基本的编程思想和良好的编码习惯与技巧。

若文章中的代码存在问题或逻辑错误，请通过邮件等形式（见文章结尾）告知于本文作者以便及时修正错误或改进代码。

算法系列文章不可避免地会参考和学习众多网友的成果，在行文风格、内容及求解思路上也会进行借鉴，如有侵权嫌疑，请联系本文作者。

PS：若为转载该文章，请务必注明来源，本站点欢迎大家转载。

问题描述

如果序列 S1 中的所有元素按照其在 S1 中的出现顺序依次出现在另一个序列 S2 中，则称 S1 为 S2 的子序列。

子序列不要求位置的连续性（即，元素相邻），只要相对顺序不变即可。

若给定一个序列集合（数量大于或等于2，但通常为两个序列），则这些序列所共同拥有的子序列，称为公共子序列。而在这些公共子序列中长度最长的子序列则称为该序列集合的最长公共子序列（Longest Common Sequence, LCS）。

本例所要求的便是求解任意两个序列的最长公共子序列（可能存在多个不同的序列），并打印其长度及其其中的任意一个序列。

例如，序列 {B,D,C,A,B,A} 和 {A,B,C,B,D,A,B} 的最长公共子序列为 {B,C,B,A} 和 {B,D,A,B} ，且其最长公共子序列的长度为4。

求解方案

动态规划法

首先，对最长公共子序列的求解过程做如下数学推导。

假设，存在序列集合 Xi={x1,x2,...,xi} 和 Yj={y1,y2,...,yj} ，其最长公共子序列为 Zk={z1,z2,...,zk} 。则存在以下情况：

• 若 xi=yj ，则有 zk=xi=yj ，且 Zk−1={z1,z2,...,zk−1} 是 Xi−1={x1,x2,...,xi−1} 与 Yj−1={y1,y2,...,yj−1} 的一个最长公共子序列
• 若 xi≠yj ，则若 zk≠xi ，那么， Zk 是 Xi−1 与 Yj 的一个最长公共子序列。注：此时 zk 不一定等于 yj ，但该推论是包含等于或不等于的情况的
• 若 xi≠yj ，则若 zk≠yj ，那么， Zk 是 Xi 与 Yj−1 的一个最长公共子序列。注：此时 zk 不一定等于 xi ，但该推论是包含等于或不等于的情况的

根据以上推论可进一步推断以下求解过程是与其等效的：

• 当 xi=yj 时，首先找出 Xi−1 与 Yj−1 的最长公共子序列，再在该子序列后面加上 xi 或 yj ，而后所得的子序列即为 Xi 与 Yj 的最长公共子序列
• 而当 xi≠yj 时，就需要分别求解 Xi−1 与 Yj 以及 Xi 与 Yj−1 的最长公共子序列，最后，所得的这两个子序列中的较长者即为 Xi 与 Yj 的最长公共子序列

若用 ∏(i,j) 表示 Xi 与 Yj 的最长公共子序列，那么，将有如下公式成立：

∏(i,j)={∏(i−1,j−1)+xi,xi=yjmax{∏(i−1,j),∏(i,j−1)},xi≠yj,i≥1,j≥1

注意，公式中的加号表示序列与元素的连接，而不是数值的加减。
当 i 与 j 为 1 时，上面的公式将出现 ∏(0,0) ，而其正好表示的是 Xi−1 与 Yj−1 的最长公共子序列为空序列，且其长度为 0 。

从以上公式可以发现最长公共子序列问题具有子问题重叠的性质。因为，在求解 Xi 与 Yj 的最长公共子序列时，需要分别求解 Xi−1 与 Yj 以及 Xi 与 Yj−1 的最长公共子序列，而这两个子问题都包含一个公共子问题，即，求解 Xi−1 与 Yj−1 的最长公共子序列。

因此，可以采用动态规划法来求解最长公共子序列问题。

动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费时间。（引用自「维基百科」）

但是，若要寻找最长公共子序列，需要首先计算公共子序列的长度，再根据长度及坐标位置回溯才能寻找出 Xi 和 Yj 的最长公共子序列。

因此，如果用二位数组 f[i][j] 表示序列 Xi 和 Yj 的最长公共子序列的长度，那么根据前面的最长公共子序列的求解公式，便可相应地推导出求解最长公共子序列的长度的公式，即：

f[i][j]={0,i=0或j=0f[i−1][j−1]+1,i≥1,j≥1且xi=yjmax{f[i−1][j],f[i][j−1]},i≥1,j≥1且xi≠yj

这样， f[i][j] 中的最大值便是 Xi 和 Yj 的最长公共子序列的长度，而根据该数组回溯，便可找到该最长公共子序列。

以序列 Xi={A,B,C,B,D,A,B} 和 Yj={B,D,C,A,B,A} 为例，可以通过下图了解整个求解最长公共子序列长度的过程：

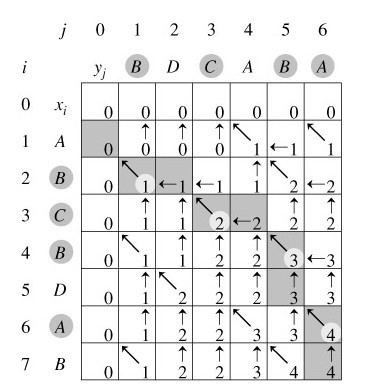
上图取自于 https://blog.csdn.net/v_JULY_v/article/details/6110269

这里直接给出实现代码，可以结合上图与代码进行分析（时间复杂度为 O(mn) ）：

#define MAX_SEQ_LEN 50

typedef enum {
    LEN_DIR_LEFT,
    LEN_DIR_TOP,
    LEN_DIR_TOP_LEFT
} LCSLenDir;

typedef struct _LCSLen {
    // 最长公共子序列的长度
    int value;
    // 长度求值基于哪个方向的结果，
    // 沿着该方向回溯便可反向找出对应的最长公共子序列
    LCSLenDir dir;
} LCSLen;

// Note：二维数组作为参数时，必须指定第二维的长度
void lcs_search_dynamic_programming(
    LCSLen lcs_len[][MAX_SEQ_LEN]
    , int seq_x[], int seq_y[]
    , int seq_x_len, int seq_y_len
) {
    // 将(i,0)的单元格全部置为0
    for (int i = 0; i <= seq_x_len; i++) {
        lcs_len[i][0].value = 0;
    }
    // 将(0,j)的单元格全部置为0
    for (int j = 0; j <= seq_y_len; j++) {
        lcs_len[0][j].value = 0;
    }

    // 沿着二维数组的i轴从上到下依次沿着j轴从左到右计算公共子序列的长度
    for (int i = 1; i <= seq_x_len; i++) {
        for (int j = 1; j <= seq_y_len; j++) {
            // f[i][j] = f[i-1][j-1] + 1, x[i] = y[j]
            // Note：数组seq_x与seq_y的元素是从0开始的
            if (seq_x[i - 1] == seq_y[j - 1]) {
                lcs_len[i][j].value = lcs_len[i - 1][j - 1].value + 1;
                lcs_len[i][j].dir = LEN_DIR_TOP_LEFT;
            }
            // f[i][j] = max(f[i-1][j], f[i][j-1])
            else if (lcs_len[i - 1][j].value >= lcs_len[i][j - 1].value) {
                lcs_len[i][j].value = lcs_len[i - 1][j].value;
                lcs_len[i][j].dir = LEN_DIR_TOP;
            } else {
                lcs_len[i][j].value = lcs_len[i][j - 1].value;
                lcs_len[i][j].dir = LEN_DIR_LEFT;
            }
        }
    }
}

注意：

• 这里通过结构体LCSLen同时记录最长公共子序列的长度和方向，避免传递多个数组，可提升可读性
• 对于多个意义相同的固定的常量值，为其定义枚举类型，是一种良好的编码习惯
• 这里没有将i和j定义为函数的局部变量是为了在阅读时不用担心二者的值会被前面的逻辑所影响，因为前后的变量具有不同的作用域且是相互独立的。从而确保阅读的流畅性，同时，代码本身逻辑的内聚性也更强
• 需在确保良好的阅读体验的情况下对初始数据、方法参数列表等进行合理换行，避免在网页中出现横向滚动条，保证一眼可以看到全部内容

在得到最长公共子序列的长度的二维数组后，便可从最右下角位置开始回溯并打印最长公共子序列（时间复杂度为 O(m+n) ）：

void print_lcs(LCSLen lcs_len[][MAX_SEQ_LEN], int seq_x[], int i, int j) {
    if (i == 0 || j == 0) {
        return;
    }

    if (lcs_len[i][j].dir == LEN_DIR_TOP_LEFT) {
        print_lcs(lcs_len, seq_x, i - 1, j - 1);
        // Note：i为序列X的下表，
        // 若要打印序列Y的元素，则应为 seq_y[j-1]
        printf("%c ", seq_x[i - 1]);
    }
    else if(lcs_len[i][j].dir == LEN_DIR_TOP) {
        print_lcs(lcs_len, seq_x, i - 1, j);
    }
    else {
        print_lcs(lcs_len, seq_x, i, j - 1);
    }
}

参考

• 动态规划算法解最长公共子序列LCS问题：详细讲解了动态规划法的实现过程并给出了对空间复杂度进行优化后的实现代码
• 动态规划最长公共子序列过程图解：图例丰富有助于理解求解的动态过程
• 算法导论-最长公共子序列LCS（动态规划）：介绍了蛮力搜索和动态规划两种方式，也同样给出了进行空间优化后的代码（实现较前面的文章更简单、清晰）。注：蛮力搜索的时间复杂度为 O(n2m)

附录

以下为完整的各方案代码，并包含性能测试：

#include <stdio.h>
#include <stdlib.h>

#define MAX_SEQ_LEN 50

typedef enum {
    LEN_DIR_LEFT,
    LEN_DIR_TOP,
    LEN_DIR_TOP_LEFT
} LCSLenDir;

typedef struct _LCSLen {
    // 最长公共子序列的长度
    int value;
    // 长度求值基于哪个方向的结果，
    // 沿着该方向回溯便可反向找出对应的最长公共子序列
    LCSLenDir dir;
} LCSLen;

void print_lcs(LCSLen lcs_len[][MAX_SEQ_LEN], int seq_x[], int i, int j);

void lcs_search_dynamic_programming(
    LCSLen lcs_len[][MAX_SEQ_LEN]
    , int seq_x[], int seq_y[]
    , int seq_x_len, int seq_y_len
);

int main(int argc, char *argv[]) {
    int seq_x[] = {'A', 'B', 'C', 'B', 'D', 'A', 'B'};
    // int seq_x[] = {'A', 'C', 'C', 'G', 'G', 'T', 'C'
    //                 , 'G', 'A', 'G', 'T', 'G', 'C', 'G'
    //                 , 'C', 'G', 'G', 'A', 'A', 'G', 'C'
    //                 , 'C', 'G', 'G', 'C', 'C', 'G', 'A'
    //                 , 'A'};
    int seq_x_len = sizeof(seq_x) / sizeof(seq_x[0]);

    int seq_y[] = {'B', 'D', 'C', 'A', 'B', 'A'};
    // int seq_y[] = {'G', 'T', 'C', 'G', 'T', 'T', 'C'
    //                 , 'G', 'G', 'A', 'A', 'T', 'G', 'C'
    //                 , 'C', 'G', 'T', 'T', 'G', 'C', 'T'
    //                 , 'C', 'T', 'G', 'T', 'A', 'A', 'A'};
    int seq_y_len = sizeof(seq_y) / sizeof(seq_y[0]);

    LCSLen lcs_len[MAX_SEQ_LEN][MAX_SEQ_LEN];

    lcs_search_dynamic_programming(lcs_len, seq_x, seq_y, seq_x_len, seq_y_len);
    printf("最长公共子序列的长度为: %d\n", lcs_len[seq_x_len][seq_y_len].value);

    printf("其中一个最长公共子序列为: ");
    print_lcs(lcs_len, seq_x, seq_x_len, seq_y_len);
    printf("\n");

    return 0;
}

// Note：二维数组作为参数时，必须指定第二维的长度
void lcs_search_dynamic_programming(
    LCSLen lcs_len[][MAX_SEQ_LEN]
    , int seq_x[], int seq_y[]
    , int seq_x_len, int seq_y_len
) {
    // 将(i,0)的单元格全部置为0
    for (int i = 0; i <= seq_x_len; i++) {
        lcs_len[i][0].value = 0;
    }
    // 将(0,j)的单元格全部置为0
    for (int j = 0; j <= seq_y_len; j++) {
        lcs_len[0][j].value = 0;
    }

    // 沿着二维数组的i轴从上到下依次沿着j轴从左到右计算公共子序列的长度
    for (int i = 1; i <= seq_x_len; i++) {
        for (int j = 1; j <= seq_y_len; j++) {
            // f[i][j] = f[i-1][j-1] + 1, x[i] = y[j]
            // Note：数组seq_x与seq_y的元素是从0开始的
            if (seq_x[i - 1] == seq_y[j - 1]) {
                lcs_len[i][j].value = lcs_len[i - 1][j - 1].value + 1;
                lcs_len[i][j].dir = LEN_DIR_TOP_LEFT;
            }
            // f[i][j] = max(f[i-1][j], f[i][j-1])
            else if (lcs_len[i - 1][j].value >= lcs_len[i][j - 1].value) {
                lcs_len[i][j].value = lcs_len[i - 1][j].value;
                lcs_len[i][j].dir = LEN_DIR_TOP;
            } else {
                lcs_len[i][j].value = lcs_len[i][j - 1].value;
                lcs_len[i][j].dir = LEN_DIR_LEFT;
            }
        }
    }
}

void print_lcs(LCSLen lcs_len[][MAX_SEQ_LEN], int seq_x[], int i, int j) {
    if (i == 0 || j == 0) {
        return;
    }

    if (lcs_len[i][j].dir == LEN_DIR_TOP_LEFT) {
        print_lcs(lcs_len, seq_x, i - 1, j - 1);
        // Note：i为序列X的下表，
        // 若要打印序列Y的元素，则应为 seq_y[j-1]
        printf("%c ", seq_x[i - 1]);
    }
    else if(lcs_len[i][j].dir == LEN_DIR_TOP) {
        print_lcs(lcs_len, seq_x, i - 1, j);
    }
    else {
        print_lcs(lcs_len, seq_x, i, j - 1);
    }
}