算法分析系列文章中的代码可被任何人无偿使用于任何场景且无需注明来源也不必在使用前征得本文作者同意。

算法分析系列文章旨在传播准确、完整、简洁、易懂、规范的代码实现，并传授基本的编程思想和良好的编码习惯与技巧。

若文章中的代码存在问题或逻辑错误，请通过邮件等形式（见文章结尾）告知于本文作者以便及时修正错误或改进代码。

算法系列文章不可避免地会参考和学习众多网友的成果，在行文风格、内容及求解思路上也会进行借鉴，如有侵权嫌疑，请联系本文作者。

PS：若为转载该文章，请务必注明来源，本站点欢迎大家转载。

问题描述

从0和1开始，之后的每一个数均为前两个数的和，这样性质的数依次排列，便称为斐波那契数列。即形成如下数列形式：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

用数学公式表示该数列即为：

$$F(n) = \begin{cases} 0, & n = 0 \\ 1, & n = 1 \\ F(n - 1) + F(n - 2), & n >= 2 \end{cases}$$

本案例所要解决的就是：给定一个整数n，求解斐波那契数列中第n项的数值。注意，0表示第零项，而不是第一项。

求解方案

递归法

从斐波那契数列的数学公式可以很直观地想到通过递归方法来求解（这里仅为代码片断，详细的见附录）：

uint64_t fibonacci_recursion(uint32_t n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    }
    return fibonacci_recursion(n - 1) + fibonacci_recursion(n - 2);
}

注意：

• 这里定义数列的数值为uint64_t类型，其所能表示的最大值大于int类型的数据，从而便于计算更大长度的数列

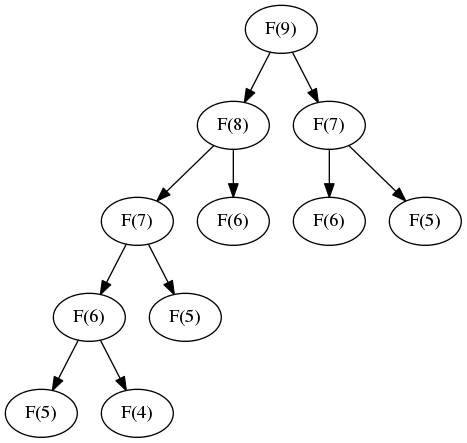
以上递归过程可以用下图展示（以n=9为例）：

Show graph description

@startdot
digraph G {
    f9 [label="F(9)"]
    f9_f8 [label="F(8)"]
    f9_f7 [label="F(7)"]
    f9_f8_f7 [label="F(7)"]
    f9_f8_f6 [label="F(6)"]
    f9_f7_f6 [label="F(6)"]
    f9_f7_f5 [label="F(5)"]
    f9_f8_f7_f6 [label="F(6)"]
    f9_f8_f7_f5 [label="F(5)"]
    f9_f8_f7_f6_f5 [label="F(5)"]
    f9_f8_f7_f6_f4 [label="F(4)"]

    f9 -> f9_f8
    f9 -> f9_f7

    f9_f8 -> f9_f8_f7
    f9_f8 -> f9_f8_f6

    f9_f7 -> f9_f7_f6
    f9_f7 -> f9_f7_f5

    f9_f8_f7 -> f9_f8_f7_f6
    f9_f8_f7 -> f9_f8_f7_f5

    f9_f8_f7_f6 -> f9_f8_f7_f6_f5
    f9_f8_f7_f6 -> f9_f8_f7_f6_f4
}
@enddot

从上图可以看出来，整个过程就是在计算二叉树的根节点的数值（=左节点数值+右节点数值）。遍历所有节点的时间复杂度为 $O(2^n)$ ，该时间复杂度也就是递归的时间复杂度。

动态规划法

从以上递归方案可以发现，在计算过程中出现了大量的重复计算，比如，在计算F(9)时需要计算F(8)与F(7)，而计算F(8)时，又要重新计算F(7)。而如果我们将F(7)的计算结果保留下来，则当F(8)计算完毕后，便可直接通过记录下来的F(7)与F(8)求和得到F(9)的结果。也就免去了对二叉树右子树的遍历过程，只需要自顶向下一直沿着左子树做遍历即可，所需时间为二叉树的高度n，时间复杂度也就变为 $O(n)$ 。

而对于包含重复求解的过程，采用动态规划法可以很好地避免该问题。

动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费时间。（引用自「维基百科」）

以下为采用动态规划法的求解代码：

// uint64_t所能表示的最大整数为18446744073709551615,
// 而数列的第94项将大于该数，故，这里限定最大只能求解第93项的数值，
// 不过，由于数组索引为0的位置表示的为数列的第0项，故，数组的实际长度应为n+1，
// 而索引位置为n的元素即为数列的第n项数值
#define MAX_FIBONACCI_SIZE 94

uint64_t fibonacci_dynamic_programming(uint32_t n) {
    static uint64_t fibonacci[MAX_FIBONACCI_SIZE] = {0, 1};

    if (n == 0) {
        return 0;
    }
    // 数列的第n项不为0时，便可认定为已经计算过该项的值，直接返回，无需继续计算
    else if (fibonacci[n] != 0) {
        return fibonacci[n];
    }
    // 按照数列的数据公式递归求解第n项的值，并将其记录在数组中，这样，在左递归完成后，便不会再继续右递归了
    else {
        fibonacci[n] = fibonacci_dynamic_programming(n - 1) + fibonacci_dynamic_programming(n - 2);
        return fibonacci[n];
    }
}

注意：

• 这里采用C语言中的静态局部变量（fibonacci）来记录过程数据，可避免从外部传递数组，以提高接口的内聚性。若需要打印数列的所有项的数值，则可从外部传入数组，再将各项结果存储在该数组中，最后按序打印即可

迭代法

可能有同学会将该方法视为动态规划法的迭代版本，但是，本文却不是很赞同。

虽然，在该迭代过程中有存储数列前一项的计算结果，但其与动态规划存在的一个不同是，动态规划中所存储的计算结果不是立即被使用的，其是在遇到对相同项求值时才被调用的，且对其也可能存在多次调用的情况，而迭代过程中的计算结果只会被使用一次而且是立即使用。

所以，本文将这两种视为不同且独立的方法。

其实，如果不考虑数学公式所造成的误导性以及对相关算法的学习的角度，而仅从对数列的描述来看，最直接的求解方法应该是迭代（即，循环）方式。因为，从第2项开始，数列的每项数值均为前两项的和。用代码表示即为：

uint64_t fibonacci_loop(uint32_t n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        // 数列的第n项
        uint64_t fib_n = 0;
        // 数列的第n-1项，初始为第1项，值为1
        uint64_t fib_n_1 = 1;
        // 数列的第n-2项，初始为第0项，值为0
        uint64_t fib_n_2 = 0;

        // 开始状态：
        // [...................n_2....n_1...n.....]
        //                      |      |    |
        // [0, 1, 1, 2, 3, 5, n - 2, n - 1, n, ...]
        // 向右平移后：
        // [.........................n_2...n_1..n.]
        //                            |     |
        // [0, 1, 1, 2, 3, 5, n - 2, n - 1, n, ...]
        for (uint32_t i = 2; i <= n; i++) {
            // 数列的第n项 = 数列的第n-1项 + 数列的第n-2项
            fib_n = fib_n_1 + fib_n_2;
            // 向右平移1项，即，
            // 上一次计算的第n-1项作为下一次计算的第n-2项，
            // 上一次计算的第n项作为下一次计算的第n-1项
            fib_n_2 = fib_n_1;
            fib_n_1 = fib_n;
        }
        return fib_n;
    }
}

从时间复杂度来看，该方法与动态规划法是一样的，二者的时间复杂度均为 $O(n)$ ，只是，从代码性能来看，迭代方式的空间复杂度为 $O(1)$ ，而且，由于递归需要消耗内存的栈空间并且调用过程中存在变量入栈出栈操作，因此，递归的性能会稍低于迭代的方式。

但是，在实际应用中，递归方式的代码会比迭代方式的代码更加直观和易读，并且其性能损耗一般可以忽略，故通常，以递归方式编写代码会更好。除非，递归的层次太深（数千上万级别的），造成线程栈空间不足时（线程的栈空间一般为固定大小，且多为几KB），这时，应该采用迭代（循环）方案去做代码实现。

参考

• Fibonacci Numbers Generator：计算斐波那契数列的站点，最大可计算数列第10000项的数值（有2090位数字）
• The Fibonacci series：列出了从0到300的斐波那契数列，可参照该数列检查以上代码计算结果的准确性
• C Programming/stdint.h：C语言的整形类型及所表示的数值范围
• How to print a int64_t type in C：如何通过printf打印uint64_t类型的值 - printf("a=%jd\n", a);
• 【算法02】3种方法求解斐波那契数列：可以了解和掌握矩阵乘法求解斐波那契数列
• LaTeX Math Symbols

附录

以下为完整的各方案代码，并包含性能测试：

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <sys/time.h>

// uint64_t所能表示的最大整数为18446744073709551615,
// 而数列的第94项将大于该数，故，这里限定最大只能求解第93项的数值，
// 不过，由于数组索引为0的位置表示的为数列的第0项，故，数组的实际长度应为n+1，
// 而索引位置为n的元素即为数列的第n项数值
#define MAX_FIBONACCI_SIZE 94

double current_timestamp();
uint64_t fibonacci_recursion(uint32_t n);
uint64_t fibonacci_dynamic_programming(uint32_t n);
uint64_t fibonacci_loop(uint32_t n);

int main(int argc, char *argv[]) {
    uint32_t n = 0;
    uint64_t fib = 0;
    double start_time, end_time;

    //printf("Max uint64_t: %ju\n", UINT64_MAX);
    printf("请输入斐波那契数列长度: ");
    scanf("%d", &n);
    if (n >= MAX_FIBONACCI_SIZE) {
        printf("得到所求数列长度为%d, 但本系统支持的最大长度为%d\n", n, MAX_FIBONACCI_SIZE - 1);
        return 1;
    }
    printf("斐波那契数列的第%d个数为:\n", n);

    if (n > 40) {
        printf("- 递归算法    : 无解（求值过于耗时！）\n");
    } else {
        start_time = current_timestamp();
        fib = fibonacci_recursion(n);
        end_time = current_timestamp();
        printf("- 递归算法    : %ju, 耗时: %f毫秒\n", fib, end_time - start_time);
    }

    // Note：需要通过格式控制符 %ju 来打印uint64_t类型的数据，
    // 否则，会出现因精度丢失而造成输出不准确的问题
    start_time = current_timestamp();
    fib = fibonacci_dynamic_programming(n);
    end_time = current_timestamp();
    printf("- 动态规划算法: %ju, 耗时: %f毫秒\n", fib, end_time - start_time);

    start_time = current_timestamp();
    fib = fibonacci_loop(n);
    end_time = current_timestamp();
    printf("- 迭代算法    : %ju, 耗时: %f毫秒\n", fib, end_time - start_time);

    return 0;
}

// 递归法求解
uint64_t fibonacci_recursion(uint32_t n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    }
    return fibonacci_recursion(n - 1) + fibonacci_recursion(n - 2);
}

// 动态规划法（Dynamic programming）求解
uint64_t fibonacci_dynamic_programming(uint32_t n) {
    static uint64_t fibonacci[MAX_FIBONACCI_SIZE] = {0, 1};

    if (n == 0) {
        return 0;
    }
    // 数列的第n项不为0时，便可认定为已经计算过该项的值，直接返回，无需继续计算
    else if (fibonacci[n] != 0) {
        return fibonacci[n];
    }
    // 按照数列的数据公式递归求解第n项的值，并将其记录在数组中，这样，在左递归完成后，便不会再继续右递归了
    else {
        fibonacci[n] = fibonacci_dynamic_programming(n - 1) + fibonacci_dynamic_programming(n - 2);
        return fibonacci[n];
    }
}

// 迭代法求解
uint64_t fibonacci_loop(uint32_t n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        // 数列的第n项
        uint64_t fib_n = 0;
        // 数列的第n-1项，初始为第1项，值为1
        uint64_t fib_n_1 = 1;
        // 数列的第n-2项，初始为第0项，值为0
        uint64_t fib_n_2 = 0;

        // 开始状态：
        // [...................n_2....n_1...n.....]
        //                      |      |    |
        // [0, 1, 1, 2, 3, 5, n - 2, n - 1, n, ...]
        // 向右平移后：
        // [.........................n_2...n_1..n.]
        //                            |     |
        // [0, 1, 1, 2, 3, 5, n - 2, n - 1, n, ...]
        for (uint32_t i = 2; i <= n; i++) {
            // 数列的第n项 = 数列的第n-1项 + 数列的第n-2项
            fib_n = fib_n_1 + fib_n_2;
            // 向右平移1项，即，
            // 上一次计算的第n-1项作为下一次计算的第n-2项，
            // 上一次计算的第n项作为下一次计算的第n-1项
            fib_n_2 = fib_n_1;
            fib_n_1 = fib_n;
        }
        return fib_n;
    }
}

// 获取当前系统时间的毫秒值
double current_timestamp() {
    struct timeval te;
    gettimeofday(&te, NULL);

    double msec = te.tv_sec * 1000.0 + (te.tv_usec / 1000.0);
    return msec;
}